- ku plotësohen kushtet
- (a1) (
 n  0) nC0 nC1nC2 ;
- (a2) Ci
 Cj  , i j, i, j0, 1, 2 ;
- (a3)
 Ck0
- Pra: 4
 7 (mod 3), 2 - 8 (mod 3), ndërsa 5  7 (mod 3).
3.3. RELACIONI I RENDITJES
- P ë r k u f i z i m i 3.3.1. - Relacioni binar ρ në A quhet relacion i renditjes, nëse është refleksiv, antisimetrik dhe transitiv.
- Relacionet e renditjes shënohen me këtë simbol
 . Relacionet më të rëndësishme të renditjes janë : plotpjesëtueshmëria (  ), nuk është më i madh ( ), nuk është më i vogël ( ) dhe inkluzionet  , .
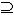- P ë r k u f i z i m i 3.3.2. - Relacioni binar ρ në A quhet relacion rigoroz i renditjes, nëse është irefleksiv, antisimetrik dhe transitiv.
- Relacione rigoroze të renditjes janë : është më i madh (>), është më i vogël (<) dhe inkluzionet
 , .
- Bashkësia A për elementet e së cilës mund të përkufizohet relacioni i renditjes , quhet bashkësi e renditur lidhur me atë relacion ose sistem i renditur dhe shënohet me (A, ).
- Kur për çdo dy elemente të bashkësisë së renditur A vlen :
ose a ρ b ose b ρ a
- thuhet se ajo bashkësi është plotësisht (linearisht) e renditur, në rast të kundërt është pjesërisht (parcialisht) e renditur.
- Për shembull, bashkësia e numrave natyralë në lidhje me relacionin > është plotësisht e renditur, ndërsa në lidhje me relacionin është pjesërisht e renditur.
3.4. RELACIONET NDËRMJET DY BASHKËSIVE
- Kemi konstatuar se çdo nënbashkësi ρ e katrorit kartezian A2 quhet relacion binar në bashkësinë A. Në analogji thuhet : nëse A, B janë dy bashkësi jo të zbrazëta, atëherë çdo nënbashkësi ρ {(a, b)
 aA bBa ρ b} e prodhimit kartezian A B quhet relacion ndërmjet bashkësive A, B.
- Në përgjithësi, nëse supozoj më se A1A, B11B, atëherë ρ A1B1( ρ AB) quhet relacion ndërmjet bashkësive A, B ku nënbashkësia A1 quhet domen, e nënbashkësia B1 kodomen i relacionit ρ .
- P.sh. për A{2,3,4}, B{1,2,3,4,5,6}
- (1) ρ 1{(2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4)}
|
