- Në formulën e fundit F(x) paraget një funksion gjykimesh me variablen x, kurse A bashkësinë e elementeve të atilla që kur cilido prej tyre zëvendësohet në F(x) e shndërron atë në gjykim të saktë.
- Me formulën a
 A përcaktohet se a është element i bashkësisë A ( a i përket bashkësisë A) dhe quhet relacion i përkatshmërisë. Negacioni i këtij relacioni shënohet : b A përcaktohet se a është element i bashkësisë A ( a i përket bashkësisë A) dhe quhet relacion i përkatshmërisë. Negacioni i këtij relacioni shënohet : b A ose A ose  (b (b A). Bashkësia që nuk e përmban asnjë element quhet bashkësi e zbrazët (vakante) dhe shënohet me simbolin A). Bashkësia që nuk e përmban asnjë element quhet bashkësi e zbrazët (vakante) dhe shënohet me simbolin  . P.sh. bashkësia e zgjidhjeve të ekuacionit x2 + 1 . P.sh. bashkësia e zgjidhjeve të ekuacionit x2 + 1  0 në fushën e numrave realë është bashkësi e zbrazët. Në matematikë rëndom shqyrtohen bashkësitë elementet e të cilave janë objekte matematikore. Bashkësitë që kanë për objekte (elemente) numra të ndryshëm quhen bashkësi numerike. Bashkësitë më të rëndësishme numerike janë: 0 në fushën e numrave realë është bashkësi e zbrazët. Në matematikë rëndom shqyrtohen bashkësitë elementet e të cilave janë objekte matematikore. Bashkësitë që kanë për objekte (elemente) numra të ndryshëm quhen bashkësi numerike. Bashkësitë më të rëndësishme numerike janë:
- (1) Bashkësia e numrave natyralë :
  { 1, 2, 3, . . . , n, n + 1, . . . } ; { 1, 2, 3, . . . , n, n + 1, . . . } ;
- (2) Bashkësia e numrave të plotë :
  { . . . , - 2, -1, 0,1, 2, . . . } ; { . . . , - 2, -1, 0,1, 2, . . . } ;
- (3) Bashkësia e numrave racionalë :
    p p  , q , q   : :
- (4) Bashkësia e numrave realë :
  {x {x - - < x < + < x < + } ; } ;
- (5) Bashkësia e numrave kompleksë :
  {x+iy {x+iy x x  , y , y  , i , i  } ; } ;
- (6) Bashkësia e numrave çiftë (parë) :
  {n {n n n   n n 2} ; 2} ;
- (7) Bashkësia e numrave tekë (cupë) :
  {n {n n n   n n 2}. 2}.
- P ë r k u f i z i m i 2.1.1. - Bashkësia A quhet nënbashkësi e bashkësisë B, nëse çdo element i bashkësisë A është njëherit element edhe i bashkësisë B (fig. 1.1.), pra:
A B B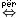 ( ( x x A):x A):x A A x x B, (...7) B, (...7)
- ku simboli
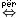 lexohet: sipas përkufzimit atëherë dhe vetëm atëherë. lexohet: sipas përkufzimit atëherë dhe vetëm atëherë.
- Formula A
 B quhet relacioni i inkluzionit ose i përfshirjes, simboli B quhet relacioni i inkluzionit ose i përfshirjes, simboli  është shenja e atij relacioni. Sinonim i relacionit A është shenja e atij relacioni. Sinonim i relacionit A B është A B është A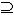 B, ku B është mbibashkësi e bashkësisë A. B, ku B është mbibashkësi e bashkësisë A.
- Nga përkufizimi 2.1.1. dalin këto dy inkluzione:
A A dhe A dhe   A (...8) A (...8)
- për çdo bashkësi A .
- Kur A
 A dhe A dhe  x x B ashtu që x B ashtu që x A, thuhet se A është nënbashkësi (pjesë) e vërtetë e bashkësisë B dhe shënohet A A, thuhet se A është nënbashkësi (pjesë) e vërtetë e bashkësisë B dhe shënohet A B. Negacioni i këtij relacioni shënohet A B. Negacioni i këtij relacioni shënohet A B. P.sh.: B. P.sh.:    , ,    , ,    , ,    , ,    , {a,b,c} , {a,b,c} {a,b,d,e,f}. {a,b,d,e,f}.
|























