Hipi Zhdripi i Matematikës/1065

4.2. INTERVALI NUMERIK DHE RRETHINA E PIKËS

Në matematikë gjatë shqyrtimit të problemeve të ndryshme shpesh jemi të udhëzuar të shfrytëzojmë jo tërë bashkësinë e numrave realë, por vetëm ndonjë nënbashkësi të vërtetë të saj. Kështu, bie fjala, kur i shqyrtojmë funksionet, pikësëpari e caktojmë zonën e përkufizimit dhe zonën e ndryshimit të tyre. Për funksione me një variabël $\scriptstyle {=}$ këto zona zakonisht janë ndonjë nënbashkësi e vërtetë e bashkësisë

\scriptstyle \mathbb {R}

të cilat quhen intervale numerike. Kështu zona e përkufizimit të funksionit $\scriptstyle {=}$ është nënbashkësia $\scriptstyle {=}$ e cila shënohet $(- 2, 2)$ dhe quhet interval, kurse zona e ndryshimit të tij është nënbashkësia $\scriptstyle {=}$ e cila shënohet $\scriptstyle {\infty }$ dhe quhet gjysmësegment ose gjysminterval.

Në përgjithësi themi:

Nëse $a$ , $b$ janë dy numra realë, ku $a < b$ , atëherë bashkësia e numrave realë $x$ që plotësojnë kushtet:

(a₁) $a x b$ quhet segment (fig. 2.1(a)) dhe shënohet $[a, b]$ , pra:

$\scriptstyle {=}$

(13)

(a₂) $a < x < b$ quhet interval (fig. 2.1.(b)) dhe shënohet $(a, b)$ , pra:

$\scriptstyle {=}$

(14)

(a₃) $a x < b$ quhet gjysmësegment ose gjysminterval (fig. 2.1.(c)) dhe shënohet $[a, b)$ , pra:

$\scriptstyle {=}$

(15)

(a₄) $a < x b$ quhet gjysmësegment ose gjysminterval (fig. 2.1.(d)) dhe shënohet $(a, b]$ , pra:

$\scriptstyle {=}$

(16)

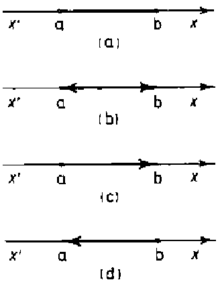
Fig. 2.1.

Pra, bashkësitë $[a, b], (a, b), [a, b),(a, b]$ quhen intervale numerike, ku numrat $a$ dhe $b$ quhen skajet (kufijtë, ekstremitetet) e intervalit numerik, kurse numri $b - a$ quhet gjatësia e intervalit numerik.

Gjeometrikisht intervali $(a, b)$ paraqitet nga bashkësia e pikave të boshtit numerik $x'x$ që shtrihen ndërmjet pikave $\scriptstyle {=}$ dhe $\scriptstyle {=}$ , pa i përfshi këto pika. Pra, për dallim nga segmenti $[a, b]$ , intervali $(a, b)$ nuk i përmban skajet $a$ dhe $b$ .

S h e m b u l l i 5 - . Në intervalet numerike