Jeni duke lexuar pjesë nga libri në punim e sipër :
Matricat dhe përcaktorët Matricat Përcaktorët Sistemet e ekuacioneve Format lineare
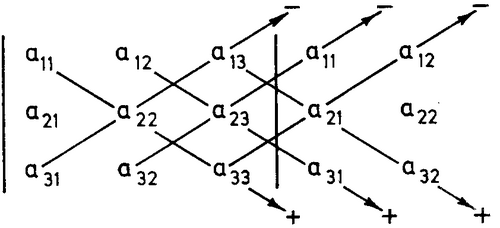
Për njehsimin e vlerës së përcaktorëve të rendit të dytë dhe të tretë rëndom shfrytëzohen këto skema:
(a)
(b)
(b1 )
(c)
Skemat (b), (b1 ) shprehin rregullën e Legendrit ose rregullën e trekëndëshit , kurse skema (c) rregullën e Sarrusit . Përdorimi i tyre shihet qartas.
Mirëpo, për njehsimin e vlerës së përcaktorëve të rendit të tretë mund të shfrytëzohet edhe vetë formula përkufizuese (25). Kur polinomin e këtij përcaktori e paraqesim në këtë trajtë:
a
11
(
a
22
a
33
−
a
23
a
32
)
−
a
12
(
a
21
a
33
−
a
23
a
31
)
+
a
13
(
a
21
a
32
−
a
22
a
31
)
{\displaystyle a_{11}(a_{22}a_{33}-a_{23}a_{32})-a_{12}(a_{21}a_{33}-a_{23}a_{31})+a_{13}(a_{21}a_{32}-a_{22}a_{31})}
respektivisht
a
11
|
a
22
a
23
a
32
a
33
|
−
a
12
|
a
21
a
23
a
31
a
33
|
+
a
13
|
a
21
a
22
a
31
a
32
|
{\displaystyle a_{11}{\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}}-a_{12}{\begin{vmatrix}a_{21}&a_{23}\\a_{31}&a_{33}\end{vmatrix}}+a_{13}{\begin{vmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{vmatrix}}}
atëherë kemi:
|
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
|
=
a
11
|
a
22
a
23
a
32
a
33
|
−
a
12
|
a
21
a
23
a
31
a
33
|
+
a
13
|
a
21
a
22
a
31
a
32
|
{\displaystyle {\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}=a_{11}{\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}}-a_{12}{\begin{vmatrix}a_{21}&a_{23}\\a_{31}&a_{33}\end{vmatrix}}+a_{13}{\begin{vmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{vmatrix}}}
ku përcaktorët e rendit të dytë:
|
a
22
a
23
a
32
a
33
|
,
|
a
21
a
23
a
31
a
33
|
,
|
a
21
a
22
a
31
a
32
|
{\displaystyle {\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}}\ ,{\begin{vmatrix}a_{21}&a_{23}\\a_{31}&a_{33}\end{vmatrix}}\ ,{\begin{vmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{vmatrix}}}
quhen subdeterminante ose minore të elementeve
a
11
,
a
12
,
a
13
{\displaystyle a_{11},a_{12},a_{13}}
det
A
{\displaystyle \det A}
D
{\displaystyle D}
a
11
,
a
12
,
a
13
{\displaystyle a_{11},a_{12},a_{13}}
D
11
,
D
12
,
D
13
{\displaystyle D_{11},D_{12},D_{13}}
D
=
a
11
D
11
−
a
12
D
12
+
a
13
D
13
{\displaystyle D=a_{11}D_{11}-a_{12}D_{12}+a_{13}D_{13}}
Kur përcaktorin e rendit të tretë e shprehim në formën (25a) ose (25b) themi se atë e kemi zhvilluar në minore (subdeterminante) sipas elementeve të rreshtit të parë. Fare lehtë mund të provohet se përcaktori
D
{\displaystyle D}
Në përgjithësi, minori që i përgjigjet elementit
a
i
k
{\displaystyle a_{ik}}
D
i
k
{\displaystyle D_{ik}}
D
i
k
{\displaystyle D_{ik}}
(
−
1
)
1
+
k
{\displaystyle (-1)^{1+k}}
kofaktor (komplementi algjebrik) i elementit
a
i
k
{\displaystyle a_{ik}}
A
i
k
{\displaystyle A_{ik}}
A
i
k
=
(
−
1
)
i
+
k
D
i
k
{\displaystyle A_{ik}=(-1)^{i+k}D_{ik}}
Duke pasur parasysh këtë, formula (25b) merr këtë trajtë:
D
=
a
11
A
11
+
a
12
A
12
+
a
13
A
13
{\displaystyle D=a_{11}A_{11}+a_{12}A_{12}+a_{13}A_{13}}
Nuk është vështirë të provohet se, në përgjithësi, përcaktori i rendit të tretë
D
{\displaystyle D}
D
=
{
a
i
1
A
i
1
+
a
i
2
A
i
2
+
a
i
3
A
i
3
(
i
=
1
,
2
,
3
)
a
1
k
A
1
k
+
a
2
k
A
2
k
+
a
3
k
A
3
k
(
k
=
1
,
2
,
3
)
{\displaystyle D={\begin{cases}a_{i1}A_{i1}+a_{i2}A_{i2}+a_{i3}A_{i3}&(i=1,2,3)\\a_{1k}A_{1k}+a_{2k}A_{2k}+a_{3k}A_{3k}&(k=1,2,3)\end{cases}}}
që quhen formulat e Laplacit [1]
Kur formulat e Laplacit i përgjithësojmë për përcaktorin e rendit
n
{\displaystyle n}
D
=
{
a
i
1
A
i
1
+
a
i
2
A
i
2
+
⋯
+
a
i
n
A
i
n
(
i
=
1
,
2
,
⋯
,
n
)
a
1
k
A
1
k
+
a
2
k
A
2
k
+
⋯
+
a
n
k
A
n
k
(
k
=
1
,
2
,
⋯
,
n
)
{\displaystyle D={\begin{cases}a_{i1}A_{i1}+a_{i2}A_{i2}+\cdots +a_{in}A_{in}&(i=1,2,\cdots ,n)\\a_{1k}A_{1k}+a_{2k}A_{2k}+\cdots +a_{nk}A_{nk}&(k=1,2,\cdots ,n)\end{cases}}}
[2] Nga këto formula shihet se njehsimi i përcaktorit të rendit
n
{\displaystyle n}
n
{\displaystyle n}
n
−
1
{\displaystyle n-1}
Të njehsohet vlera e përcaktorit
D
=
|
a
2
2
a
b
b
2
a
c
a
d
+
b
c
b
d
c
2
2
c
d
d
2
|
{\displaystyle D={\begin{vmatrix}a^{2}&2ab&b^{2}\\ac&ad+bc&bd\\c^{2}&2cd&d^{2}\end{vmatrix}}}
Z g j i d h j e: E zhvillojmë përcaktorin në minore sipas elementeve të rreshtit të dytë dhe njëherit aplikojmë vetitë e përcaktorëve siç vijon;
D
{\displaystyle D\,}
=
−
a
c
|
2
a
b
b
2
2
c
d
d
2
|
+
(
a
d
+
b
c
)
|
a
2
b
2
c
2
d
2
|
−
b
d
|
a
2
2
a
b
c
2
2
c
d
|
{\displaystyle =-ac{\begin{vmatrix}2ab&b^{2}\\2cd&d^{2}\end{vmatrix}}+(ad+bc){\begin{vmatrix}a^{2}&b^{2}\\c^{2}&d^{2}\end{vmatrix}}-bd{\begin{vmatrix}a^{2}&2ab\\c^{2}&2cd\end{vmatrix}}}
=
−
2
a
b
c
d
|
a
b
c
d
|
+
(
a
d
+
b
c
)
|
a
2
b
2
c
2
d
2
|
−
2
a
b
c
d
|
a
b
c
d
|
{\displaystyle =-2abcd{\begin{vmatrix}a&b\\c&d\end{vmatrix}}+(ad+bc){\begin{vmatrix}a^{2}&b^{2}\\c^{2}&d^{2}\end{vmatrix}}-2abcd{\begin{vmatrix}a&b\\c&d\end{vmatrix}}}
=
−
4
a
b
c
d
|
a
b
c
d
|
+
(
a
d
+
b
c
)
(
a
2
d
2
−
b
2
c
2
)
{\displaystyle =-4abcd{\begin{vmatrix}a&b\\c&d\end{vmatrix}}+(ad+bc)(a^{2}d^{2}-b^{2}c^{2})}
=
−
4
a
b
c
d
(
a
d
−
b
c
)
+
(
a
d
−
b
c
)
2
(
a
d
−
b
c
)
{\displaystyle =-4abcd(ad-bc)+(ad-bc)^{2}(ad-bc)\,}
=
(
a
d
−
b
c
)
[
(
a
d
−
b
c
)
3
−
4
a
b
c
d
]
=
(
a
d
−
b
c
)
3
{\displaystyle =(ad-bc)[(ad-bc)^{3}-4abcd]=(ad-bc)^{3}\,}
Të vërtetohet identiteti
|
a
−
b
−
c
2
a
2
a
2
b
b
−
c
−
a
2
b
2
c
2
c
c
−
a
−
b
|
=
(
a
+
b
+
c
)
3
{\displaystyle {\begin{vmatrix}a-b-c&2a&2a\\2b&b-c-a&2b\\2c&2c&c-a-b\end{vmatrix}}=(a+b+c)^{3}}
V ë r t e t i m: Duke shfrytëzuar vetitë e përcaktorëve kryhen këto transformime identike
|
a
−
b
−
c
2
a
2
a
2
b
b
−
c
−
a
2
b
2
c
2
c
c
−
a
−
b
|
{\displaystyle {\begin{vmatrix}a\!-\!b\!-\!c&2a&2a\\2b&b\!-\!c\!-\!a&2b\\2c&2c&c\!-\!a-\!b\end{vmatrix}}}
=
i
+
(
i
i
+
i
i
i
)
{\displaystyle \!=\!i\!+\!(ii\!+\!iii)}
|
a
+
b
+
c
a
+
b
+
c
a
+
b
+
c
2
b
b
−
c
−
a
2
b
2
c
2
c
c
−
a
−
b
|
{\displaystyle {\begin{vmatrix}a\!+\!b\!+\!c&a\!+\!b\!+\!c&a\!+\!b\!+\!c\\2b&b\!-\!c\!-\!a&2b\\2c&2c&\!c\!-\!a\!-\!b\end{vmatrix}}}
=
(
a
+
b
+
c
)
{\displaystyle \!=(a\!+\!b\!+\!c)}
|
1
l
1
2
b
b
−
c
−
a
2
b
2
c
2
c
c
−
a
−
b
|
{\displaystyle {\begin{vmatrix}1&l&1\\2b&b\!-\!c\!-\!a&2b\\2c&2c&c\!-\!a\!-\!b\end{vmatrix}}}
=
(
a
+
b
+
c
)
{\displaystyle =(a\!+\!b\!+\!c)}
|
1
0
(
i
i
−
i
)
0
(
i
i
i
−
i
)
2
b
−
(
a
+
b
+
c
)
0
2
c
0
−
(
a
+
b
+
c
)
|
{\displaystyle {\begin{vmatrix}1&{\overset {(ii-i)}{0}}&{\overset {(iii-i)}{0}}\\2b&-(a\!+\!b\!+\!c)&0\\2c&0&-(a\!+\!b\!+\!c)\end{vmatrix}}}
=
(
a
+
b
+
c
)
{\displaystyle =(a\!+\!b\!+\!c)}
|
−
(
a
+
b
+
c
)
0
0
−
(
a
+
b
+
c
)
|
{\displaystyle {\begin{vmatrix}-(\!a\!+\!b\!+\!c\!)&0\\0&-(a+b+c)\end{vmatrix}}}
=
(
a
+
b
+
c
)
3
{\displaystyle =(a\!+\!b\!+\!c)^{3}\,}
↑ 4) Sipas emrit të matematikanit të shquar francez Pilere Simon de Laplace (1749-1827).
↑ 5) Vërtetimin e këtyre formulave mund ta gjeni në [21), fq. 85-87.
![{\displaystyle =(ad-bc)[(ad-bc)^{3}-4abcd]=(ad-bc)^{3}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb37749980b1a010cd21b0823ad514b3408fffd4)
